
A Cellular Automata Model written in HTML and JavaScript
ECG Simulation display written in Java
MODEL FEATURES
This computer program attempts to simulate the properties of the specialized conduction system of the heart in a World Wide Web interface that is easily configurable in order to observe different phenomena of cardiac activation. Parameters that are user adjustable include the specification of blockage in certain regions of the system, scaling of time to help accommodate slower computer processors and to aid in the analysis of the sequence and timing of activation automaticity period of the SA Node, AV Node, and Purkinje, and a pacing option to artificially pace several regions at a given rate.
In order to most accurately simulate the actual properties of the specialized conduction system, the program uses an algorithm which first initializes parameters of each element. Next, the program determines if the appropriate elements will fire themselves if automaticity conditions are met. Finally, each element checks on its neighboring elements to see if they are stimulated. If the element itself is not stimulated and is past its refractory period, then it becomes activated. After each element is activated, it goes through its action potential depending on its activating and recovering properties, independent of adjacent tissue. Upon each change of state, the program updates the image appropriately.
An ECG simulation graph was added to demonstrate what a typical electrocardiogram might look like under the conditions shown in the automata model. The formation of the potentials measured by the ECG, based on activity in the electrical sources of the heart, is the forward problem of electrocardiography.
Theoretically, the signals measured by an actual ECG instrument are produced by changes in electrical potentials of the cardiac tissue as measured by body surface electrodes. The extracellular potential caused by an action potential along a fiber is described by the following equation:
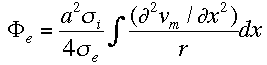
(from Bioelectricity: A Quatintative Approach by Robert Plonsey and Roger C. Barr, 1988.)
In a one-dimensional model such as this automata model, this equation can be approximated by setting extracellular potential directly proportional to the change in voltage of the source. This is the basis for the algorithm which calculates the ECG in the model. When excitable tissue is activated, initially there is a very rapid rise in transmembrane potential. During repolarization of the fiber, the change in transmembrane potential is not as large. Hence, changes in extracellular potential are due to activation and repolarization of the heart tissue.
In this simulation, when an automata element activates, it changes the potential of the source a certain amount relative to its size and other properties. When the same element repolarizes, it again changes the potential of the source. By finding how much the source voltage changes over a fixed amount of time (dv/dt), we can determine how much extracellular potential would change in relationship. Thus, we can assign values to how much the transmembrane voltage would change when an element is activated and repolarized (scaling the values in proportion to the size of the element), and use these values to determine dv/dt. dv/dt is then scaled and is plotted through a Java applet to reflect what the ECG might look like. Please note that the model does not take into account the directionality of dipoles, and as a result there are no negative deflections in the ECG simulation.
Pragmatic Notes:
The program itself is written in JavaScript1.1 and requires Netscape Navigator Version 3.0 or higher to view. There are several images which must be loaded before the program can be executed. Please wait for the document to completely load before running the simulation - this may require several minutes, depending on network load, the speed of your computer, and the speed of your internet connection.
Because the actual process of cardiac conduction system activation is in the order of milliseconds while compute intensive procedures and image updating may require more than this amount of time (particularly on slow CPUs), a time scaling factor of x10 or more is recommended. This will allow for both accurate representation of the model and will aid in observation of the process. For example, a Sun Sparc 5 should be able to provide an accurate simulation with a time factor of 20. However, slower machines such as non-Pentium PC's or non-PowerPC Macintoshes may require a time factor as high as 50 or 100.
The activity progress can also be monitored by comparing activity to the time-scaled timer in the bottom of the window (in the window status bar - please note that this timer does not work very well on the Xwindows version of Netscape.
The ECG display was written in Java and requires Java to be enabled in the browser; please note, however, that it does not work in the Xwindows version of Netscape 3.0.
Wesley Joe 5/3/97